Realtime Silhouette Rendering with Consistent Geometric Fins

Background
Cel shading is a common shading technique designed to make 3D geometry look like it was hand painted in a traditional way. While it is fairly trivial to darken vertices on the silhouette, to truly emulate the effect of a hand drawn outline, the ink outline must extend outside the silhouette of the object at a constant thickness for it to appear plausible. Games like Borderlands make liberal use of outline geometry to enhance the non-photorealistic style of the game.
My starting point was the blog post by Philip Rideout in which gaps between fins are blended using a blurring pass, which seemed wasteful, and may prohibit procedural outline effects like glowing or outline particles.
I started from scratch, but what I ended up with is a method similar to Single Pass GPU Stylized Edges by Hermosilla and Vazquez, although implemented on the geometry shader, and also requiring about half the additional geometry. I would also argue that the method I’ve produced here is considerably simpler than any previous method.
What is the Silhouette?
This is probably a good place to start. Assume for the moment that we have some nice continuous object (not a triangle mesh) like a perfect sphere. The silhouette is effectively a connected curve around the object where the surface of the object is exactly orthogonal to the direction of the viewer. Consider the horizon - the silhouette is the exact point at which the ground meets the sky.
Based on this we could formulate a simple definition of the silhouette as the set of all points \(x\) for which \(\mathbf{v}_x \cdot \mathbf{n}_x = 0 \), where \(\mathbf{v}_x\) is the view vector from the eye to \(x\) and \(\mathbf{n}_x\) is the normal at the point \(x\).
Method Overview
Determining the silhouette of a triangle mesh
Now lets consider this on a triangle mesh. Any silhouette is only going exist between points on two edges of a subset of triangles on the mesh. We will assume that our triangle mesh is sufficiently dense so we can approximate the silhouette across the triangle face with a straight line (it would be possible to generate smoother curves using a Bezier spline or equivalent). The comparison of the discrete and the continuous silhouette case is demonstrated in the figure below:
Remember that a triangle mesh is typically an approximation of some smoother surface representation, and should in most cases have vertex normals defined which effectively allow us to generate smooth shading across each face, giving the illusion of a continuous surface representation. We can use this knowledge to determine which faces are on the silhouette.
Consider an edge with vertices at \(p_{0,1} \) with vertex normals \( \mathbf{n}_{0,1} \) respectively. If \(\mathbf{v}_0 \cdot \mathbf{n}_0 < 0 \) and \(\mathbf{v}_1 \cdot \mathbf{n}_1 > 0 \) (or visa versa), then somewhere along this edge there is an \(x\) for which \(\mathbf{v}_x \cdot \mathbf{n}_x = 0 \).
A wary reader will note that \(\mathbf{v}_0 \neq \mathbf{v}_1\) which might cause problems, but as we will see, all view vectors \(\mathbf{v}_x\) will be the same \(\forall x\).
Interpolation
So we need to find the point \(x\) across the edge for which \(\mathbf{v}_x \cdot \mathbf{n}_x = 0 \). We’re going to make a couple of assumptions to simplify things. The first assumption is that we’re going to use simple linear interpolation for performance reasons. Accuracy will be affected, but we’re going to assume that the input mesh is dense and any accuracy issues will not be noticeable.
Linear interpolation would imply that we’re looking for some \(t\) for which \((1-t)\mathbf{v}_0 \cdot \mathbf{n}_0 + t \mathbf{v}_1 \cdot \mathbf{n}_1 = \mathbf{v}_x \cdot \mathbf{n}_x = 0 \), e.g. the interpolation parameter for which the the normal is zero.
The second assumption we’ll be creating the geometry of the fin on the geometry shader, which means that by convention we can rely on the fact that the geometry has already been projected, which means it already lives within a canonical viewing volume. We can now reliably state that \(\mathbf{v}_0 = \mathbf{v}_1 = [0,0,-1]^T\), i.e. the view vector for all vertices is just from the origin looking in the \(-z\) direction by the OpenGL camera convention.
So this means that we can simplify the formulation significantly to just \( (1-t) \mathbf{n}_{(0,z)} + t\mathbf{n}_{(1,z)} = 0 \), which yields \( t = -\mathbf{n}_{(0,z)} / (\mathbf{n}_{(1,z)}-\mathbf{n}_{(0,z)}) \). Built into this formula is also the implicit test: \( 0 \leq t \leq 1 \implies \) the edge crosses the silhouette.
Below is this trivial function as implemented in the geometry shader:
/** This is where most of the magic happens - it determines the interpolation value
* based on the z values of the two normals in order to detemrine a normal pointing
* out orthogonal to the view direction.
* \param n0,n1 The two input normals
* \return The output interpolation value (between 0 and 1 if edge is on the silhouette)
*/
float isSilhouette(in vec3 n0, in vec3 n1) {
// Trivial case: the normals are the same, so we'll just pick a point in the middle
if (n1.z == n0.z) {
return 0.5;
} else {
// Use our formula to determine the interpolation value and return a boolean based
// on whether the interpolant is within the two input vectors
return - n0.z / (n1.z - n0.z);
}
}
Putting it together
The geometry shader to generate fins accepts a triangle as input and spawns a triangle strip of 4 vertices as output. Each triangle is going to be processed, and we can expect neighbouring triangles on the silhouette to be consistent - see the image below for an example (I appreciate that it’s not great):
The geometry shader iterates over all edges of the triangle and determines the value of \(t\) to see if it lies on the silhouette. If it does, a fin vertex and normal is determined using a straight linear interpolation (via the built-in mix function):
// Iterate over all the edges in our triangle
int j;
for (int i = 0; i < 3; ++i) {
j = (i+1)%3;
t[cnt] = isSilhouette(normal[i], normal[j]);
if ((t[cnt] >= 0.0) && (t[cnt] <= 1.0)) {
finVerts[cnt] = mix(pos[i], pos[j], t[cnt]);
finNorms[cnt] = normalize(mix(normal[i], normal[j], t[cnt]));
++cnt;
}
}
I did also experiment with higher order mixing methods, but these showed no discernable improvement and just added significantly to the computation cost and complexity so these approaches were scrapped.
Now if the variable cnt is exactly 2 then we know that this triangle cuts the silhouette and we need to generate a triangle strip fin:
// If count is less than 2 don't do anything as there isn't a fin
if (cnt >= 2) {
// Create our triangle strip from the two input vertices and normals
finColour = vec4(0,0,0,1); // You might want to visualise something with the color
gl_Position = vec4(finVerts[0],1.0);
EmitVertex();
gl_Position = vec4(finVerts[1],1.0);
EmitVertex();
gl_Position = vec4(finVerts[0] + finScale * finNorms[0],1.0);
EmitVertex();
gl_Position = vec4(finVerts[1] + finScale * finNorms[1],1.0);
EmitVertex();
EndPrimitive();
}
Note that the rendering of the fin is an additional render pass performed after you’ve rendered the main geometry, as the geometry shader will effectively “eat” the original geometry.
Results
Here are a couple of Buddha’s of various levels of thickness:
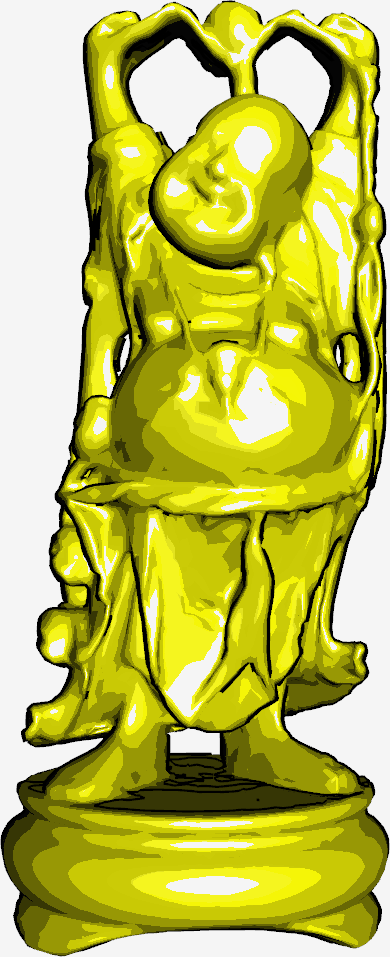 |  |  |
The results are close to perfect: the fins are consistent about both internal and external silhouettes. There are still a couple of problems which need resolving:
- The normals are not transformed correctly after projection. This is because the normals are needed in the world coordinates for the lighting calculations. You can see the error in that the line is not the same width everywhere on the silhouette. Unfortunately I’ve not yet figured out the correct method to transform the normals to be correct according to the canonical viewing volume - feel free to contact me if you have a solution to this.
- The lines don’t taper when nearing the edge of an internal silhouette (leading to “sharpy edges”). This could be fixed by tiling a round texture map on the silhouette so the borders become rounded.
- I have not explored all the fun effects that fins can do, like glow or illustrative visualisation: this is up to you!
Downloads
The source code is hosted on GitHub. Clone it from the repository using the following command from your console:
git clone https://github.com/rsouthern/Examples
This example is under rendering/fins.